Description

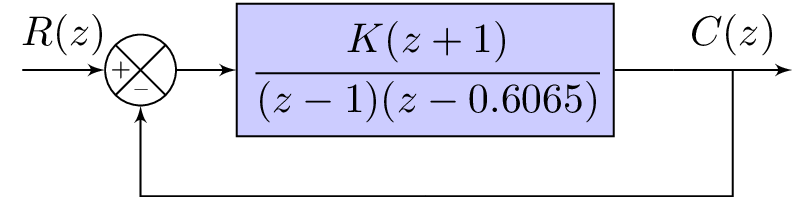
% Latex diagram produces diagram for the following question
% Consider the digital control system shown below. Plot the root loci as the gain K is varied from $0$ to $\infty$. Determine the critical value of gain K for stability. The sampling period is 0.1 sec, or $T=0.1$ What value of gain K will yield a damping ration $\zeta$ of the closed-loop poles equal to 0.5? With gain K set to yield $\zeta=0.5$, determine the damped natural frequency $\omega_d$ and the number of samples per cycle of damped sinusoidal oscillation.
 
% Numerical Answer in latex
% When $K=0.0646, \zeta=0.5$ with the pole at $z=0.771+j0.277=|0.8192|e^{j19.7620^\circ}$. 
% \begin{align*}
% z=  & |e^{-T(\zeta \omega_n)} |e^{T \omega_d} = |0.8192|e^{j19.7620^\circ} \\
% & \omega_n = \frac{\ln(0.8192)}{(-0.1)(0.5)}=3.98854 = 4 \ \text{rad/s} \\
% & \omega_d = \frac{(19.7629^\circ)}{0.1} = 3.449 \quad  \omega_d = \omega_n \sqrt{1-\zeta^2}=3.988 (0.866025)=3.4537 \ \text{rad/s} \\
% & \text{Number of Samples per Cycle } = \frac{360^\circ}{T\omega_d}=\frac{360^\circ}{19.7629^\circ}=18.22
% \end{align*}
 
\documentclass[%
% border=1pt
border={-25pt 0pt 0pt 0pt} % left bottom right top
]{standalone}
\usepackage{amsmath}
\usepackage{tikz}
\usetikzlibrary{positioning}
\usetikzlibrary{shapes,arrows,calc} 
\usetikzlibrary{decorations.text}
\tikzset{add/.style n args={4}{
		minimum width=6mm,
		path picture={
			\draw[black] 
			(path picture bounding box.south east) -- (path picture bounding box.north west)
			(path picture bounding box.south west) -- (path picture bounding box.north east);
			\node at ($(path picture bounding box.south)+(0,0.13)$)     {\tiny #1};
			\node at ($(path picture bounding box.west)+(0.13,0)$)      {\tiny #2};
			\node at ($(path picture bounding box.north)+(0,-0.13)$)        {\tiny #3};
			\node at ($(path picture bounding box.east)+(-0.13,0)$)     {\tiny #4};
		}
	}
}
\begin{document}
	
	%\begin{figure}
	%\centering
	\tikzstyle{block} = [draw, fill=blue!20, rectangle, minimum height=3em, minimum width=4em]
	\tikzstyle{controller} = [draw, fill=red!20, rectangle, minimum height=3em, minimum width=4em]
	\tikzstyle{sum} = [draw, fill=blue!20, circle, node distance=1cm]
	\tikzstyle{input} = [coordinate]
	\tikzstyle{output} = [coordinate]
	\tikzstyle{sampleSP} = [coordinate]
	\tikzstyle{sampleEP} = [coordinate]
	\tikzstyle{otherPoint} = [coordinate]
	\begin{tikzpicture}[auto, >=latex']
	% Nodes
	\node [input] (input) {};
	%\node [sum, right = 1cm of input] (sum) {};
	\node[draw,circle,add={--}{+}{}{},right of= input](sum){}; 
	%\node [sampleSP, right = 1cm of sum] (sumSP) {};
	%\node [sampleEP, right = 1cm of sumSP] (sumEP) {};
	%\node [sampleEP, above = 1cm of sumEP] (sumEPTOP) {};
	\node [block, right = 0.5cm of sum] (system) {$\cfrac{K(z+1)}{(z-1)(z-0.6065)}$}; % node[label=below:$b_1$,draw]{};
	%\node [below = 0.005 cm of system] (PointHeader) {\scriptsize{$G(s)$}};
	\node [otherPoint,right = 0.5cm of system] (branchPoint) {};
	\node [otherPoint,below = 0.5 cm of system] (belowsystem) {}; %{$\frac{1}{Ts+1}$};
	%\node [block, right = 1cm of system] (system2) {$\frac{1}{Ts+1}$};
	\node [output, right = 1cm of branchPoint] (output) {};
	\node [input, below = 0.5cm of system] (m) {};
	%\node [otherPoint, right = 1.25 of belowsystem] (systemRightDownP) {$H_1(s)$};
	
	% Second Sampler Point
	%\node [sampleSP, below = 0.5cm of systemRightDownP] (sysHSP2) {};
	%\node [sampleEP, left = 1cm of sysHSP2] (sysHEP2) {};
	%\node [sampleEP, above = 1cm of sysHEP2] (sumEPTOP2) {};
	
	% Second block 
	%\node [block, left = 0.75cm of sysHEP2] (systemH2) {$\cfrac{1-e^{-Ts}}{s}$};
	% Arrows
	\draw [draw,->] (input) -- node {$R(z)$} (sum);
	% Arrows for first sampler
	%	\draw [-] (sum) -- node {$E(s)$} (sumSP);
	%	\draw [-,thick] (sumEPTOP) -- node {$\delta_\tau$} (sumSP);
	
	%\draw [->] (sum) -- node {$E(s)$} (system);
	\draw [->] (sum) -- node {} (system);
	%Arrows for second sampler (bottom)
	%	\draw [-]  (sysHSP2)-- node {$M(s)$} (systemH);  
	%\draw [-,thick] (sysHSP2) -- node {$\delta_\tau$} (sumEPTOP2);
	%\draw [->] (sumEP) -- node {$M^\ast(s)$} (systemH);
	% \draw [->] (system) --  (system2);
	\draw [-] (system) --  (branchPoint);
	\draw [->] (branchPoint) -- node (y) {$C(z)$}(output);
	%\draw [-] (y) |- (sysHSP2) {};
	\draw [-] (y) |- (m) {} ;
	%\draw [<-] (systemH2) -- node {$M^\ast(s)$} (sysHEP2);
	%\draw [->] (sysHEP2) -- (systemH2);
	%\draw [->] (systemH2) -| node [near end] {$B(s)$} (sum) ; %{$-$}  node [near end] {} (sum);
	%\node [otherPoint, below = 1.25cm of sum] (Text) {$B(s)$};
	\draw [->] (m) -| node[pos=0.99] {} node [near end] {} (sum); %{$-$}  node [near end] {} (sum);
	\end{tikzpicture}
	%\end{figure}
\end{document}